Definisi Stack
— Stack = tumpukan
— Stack = tehnik pengambilan data ke dan dari memori
— Konsep stack
— FILO (first in last out)
— LIFO (last in first out)
Cara kerja stack
— CREATE (S) = membuat
stack
— PUSH =
menambah isi ke dalam stack
— POP =
menghapus isi stack satu-persatu
— CLEAR (S) =
mengosongkan seluruh isi stack
Macam-macam stack
— 1. satu array untuk
satu stack
— 2. satu array untuk
2 stack
a.
kedua stack pada index terkecil
b.
stack 1 pada index terkecil, stack 2 pada index terbesar
c.
kedua stack berada di tengah
Satu array untuk satu stack
— Buatlah satu buah stack dengan satu array, lalu masukan data “R
O M A N” ke dalam stack, kemudian hapus data tersebut secara satu-persatu,
dengan maksimal jumlah elemen stack = 4, dan panjang elemen 1, serta alamat
awal data adalah 1000.
— Cara membuat ???
Susunan :
— Buat stack
— Masukan kata “R O M A N”
— Hapus kata “R O M A N”
Masukan kata “R O M A N”
PUSH (“N”, S)
Pemasukan data “N” tidak dapat
dilaksanakan, karena alokasi memori yang sudah penuh.
Kesalahan semacam ini dinamakan overflow
error , yaitu pemasukan data kedalam stack yang telah penuh.
Ulangi hapus kata “R O M A”
POP (“A”, S)
Penghapusan data “A” tidak dapat
dilaksanakan, karena stack sudah dalam keadaan kosong.
Kesalahan semacam ini dinamakan underflow
error , yaitu penghapusan data di dalam stack yang sudah kosong.
Satu array untuk dua stack
— Dengan kedua stack berada pada index terkecil
— Ket : stack satu selalu berada diatas stack dua
— Ex : buatlah 2 buah stack dengan keduanya berada pada index
terkecil, lalu masukan data berikut, serta hapus secara satu persatu :
— “1, 2, 3” untuk stack satu
— “4, 5, 6” untuk stack dua
— Dengan maksimal jumlah elemen = 7, panjang elemen = 3, dan
alamat awal = 1000
Susunan :
— Buat 2 buah stack
— Masukan data “1, 2, 3” untuk stack 1
— Masukan data “4, 5, 6” untuk stack 2
— Hapus data “1, 2, 3” untuk stack 1
— Hapus data “4, 5, 6” untuk stack 2
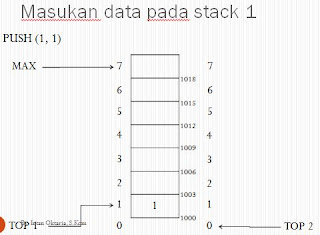
Satu array untuk dua stack
— Stack 1 pada index
terkecil, stack 2 pada index terbesar
— Ex : buatlah 2 buah stack, lalu masukan data berikut, serta
hapus secara satu persatu :
— “1, 2, 3” untuk stack satu
— “4, 5, 6” untuk stack dua
— Dengan maksimal jumlah elemen = 7, panjang elemen = 3, dan
alamat awal = 1000
Satu array untuk dua stack
— Kedua stack berada di tengah
— Ket : TOP 1 = (n/2) + 1 = (7/2) + 1 = 4
TOP 2 = (n/2) = (7/2) = 3
— Ex : buatlah 2 buah stack, lalu masukan data berikut, serta
hapus secara satu persatu :
— “1, 2, 3” untuk stack satu
— “4, 5, 6” untuk stack dua
— Dengan maksimal jumlah elemen = 7, panjang elemen = 3, dan
alamat awal = 1000
Infix dan postfix
— Contoh bentuk infix : A + B
— Contoh bentuk postfix: A B +
— A, B, C, D, etc = operand
— +, -, *, /, ^ = operator
Bagaimana jika terdapat banyak
operator???
Cara memudahkan : jadikan operand +
operator sebagai bentuk lain.
Contoh…
A + B = P = A B +
A * B = Q = A B *
Ubah ekspresi infix berikut kedalam
postfix :
( A + B ) / ( ( C – D ) * E ^ F )
( A + B ) / ( ( C – D ) * E
^ F )
= ( A + B ) / ( P * E ^ F ) = ( A + B ) / ( C D - * E ^
F )
= ( A + B ) / ( P * Q ) =
( A + B ) / ( C D - * E F ^ )
= ( A + B ) / R =
( A + B ) / C D - E F ^ *
= S / R = A B + / C D - E F ^ *
= T = A B + C D - E F ^ *
/
Tugas 2
— Ex : buatlah 2 buah stack dengan :
a)
Keduanya berada pada index
terkecil
b)
Stack 1 pada index terkecil, stack 2 pada index
terbesar
c)
Kedua stack berada di tengah
lalu masukan data berikut, serta
hapus secara satu persatu :
— stack satu : nama panggilan anda
— stack dua : nama depan ibu anda
— Dengan maksimal jumlah elemen = 15, panjang elemen = 5, dan
alamat awal = 1000